I subscribe to some of best SEO blogs and scan the email subject lines every day.
One of my favorite sections to look in for SEO news updates & tips is the SEO & SEM section in Search Engine Lands day in search.
A recent post caught my eye titled ‘Little blog scores big rankings: A Schema Creator case study’.
Firstly, lets get to understand the basics of schema micro data as it really isn’t complicated and can be highly effective in increasing search results positions and traffic to your site.
What Is Schema?
Schema is structured micro data which you display in your web pages HTML code to tell the search engines additional information about your content.
The 2 links under the next sub heading show you what type of rich data you can add to your posts and pages using a plugin or Schema creator.
Here you’ll find the most popular types of schema’s people use to add to their blogs.
Data You Can Add To Your Blog
The plugin can also automatically include http://schema.org/Blog and http://schema.org/BlogPosting schemas to your pages and posts.
It seems a little technical at first if you haven’t heard about it before but it really is quite simple.
Call it Schema, micro data or rich snippets, it doesn’t matter.
You can create the data (Schema) manually using Raven Tools Schema Creator or simply install a plugin.
Schema Micro Data Plugin
When i first found out Raven Tools had created a WordPress plugin for this task, i jumped at the chance to review the plugin and added it to my main site, WP Sites.
You can search for and download the Schema Creator by Raven plugin from the WordPress.org plugin directory or Github.
The WordPress plugin provides an easy to add your specific data to a form and embed the schema.org microdata into a WordPress post or page.
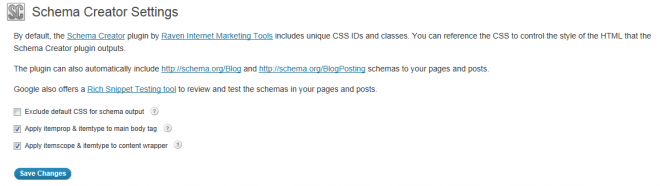
Schema Creator Plugin Settings
The plugin ads a simple setting page that you need to configure.
I simply saved these settings and left them as the defaults.
Once you activate the plugin, you also find a small icon appears above your editor.
Schema Creator Forms
Once you click the icon, you’ll get a pop up where you can choose the type of data you want to enter.
How easy is this?
Types of Forms
These several forms which have already been created so all you need to do is add your content and insert the data into your editor.
Schema Type Examples:
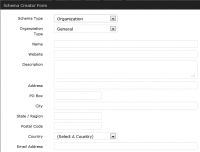
- Organization – Most important to add this data to your about page and even in your header or footer. Data you can add includes Type of Company, website, address, location etc.
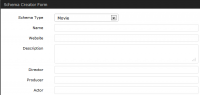
- Movie – Add information about the movie so Google understands more about your content: Name, website, movie description Director, Producer & Actor.
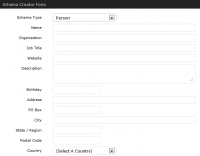
- Person – Add all your personal details in addition to your Google Plus info.
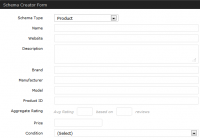
- Product – Add data which includes the brand, manufacturer, model, product i.d, price and rating.
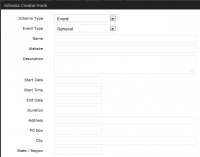
- Event – Add start and end times, duration, time and location in micro data format.
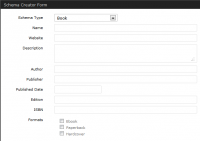
- Book – Add if its a eBook, Paperback, Hardcover, Author and publisher.
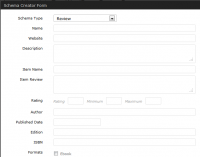
- Review – Name , review, rating, author, publication date, edition and format.
Schema Forms Gallery
Check out all the different forms you can use to add different types of micro data to your blogs posts and pages depending on the topic.
Add all the data and click insert.
Testing Schema Data
Google also offers a Rich Snippet Testing tool to review and test the micro data in your pages and posts.
I’ve already written about how to use Google’s rich snippet testing tool to verify author ownership and this tool will also check to see that any additional Schema micro data you add is valid.
WP Sites Schema Micro Data Examples
Here’s a couple of real examples i have added to WP Sites.
- Choose a Schema Type
- Add the data

Insert the data in your HTML editor
Video
Conclusion
Be nice to see Joost de Valk add this feature to WordPress SEO by Yoast considering its the best all in one SEO plugin for WordPress.



Leave a Reply
You must be logged in to post a comment.